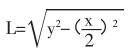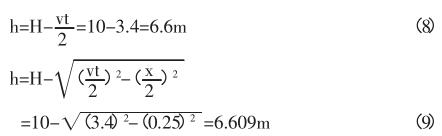摘要: 隨著現(xiàn)代科學技術的不斷提升,煤礦、鐵礦、造紙、稀土等行業(yè)的自動化水平取得飛速發(fā)展,能否穩(wěn)定、準確、智能地測量料位決定著這些行業(yè)是否能夠向現(xiàn)代化、智能化發(fā)展。測量料位的方法有很多,其中超聲波料位計采用非接觸方式,能夠有效避免光線、粉塵、煙霧和電磁干擾的影響。研究和設計精度高、穩(wěn)定性好、性價比高的超聲波液位計是充滿挑戰(zhàn)性和具有現(xiàn)實意義的課題。考慮到超聲波的傳播速度受溫度的影響較大,推導出帶有溫度補償?shù)乃俣刃拚嬎愎剑迷谲浖惴ㄖ校粸榱诉M一步提高測量精度,本文還詳細分析了超聲波傳播的實際路徑并給出了計算公式。
1 速度與溫度關系修正
超聲波在空氣中的傳播速度隨溫度的變化而變化,為了提高超聲波測量的準確度,就必須進行溫度補償,校正超聲波傳播速度。超聲波傳播速度 v 與相對溫度 T 的計算公式如下:
v=331.4+0.607T (1)
在采集環(huán)境溫度過程中,可以采用以幾種方案:
1.1 采用半導體熱敏電阻
半導體熱敏電阻是一種電阻值隨溫度變化而改變的電阻,半導體熱敏電阻大多數(shù)都是采用半導體材料經(jīng)過特殊的處理工藝制造而成的,大多數(shù)半導體熱敏電阻是負溫度系數(shù),其電阻的大小會隨著環(huán)境溫度的降低而增加。
半導體熱敏電阻的阻值受溫度的影響較大,是一種非常靈敏的溫度傳感器。但半導體熱敏電阻的線性度較差,并且與生產(chǎn)工藝有很大關系。制造商給不出標準化的熱敏電阻曲線。半導體熱敏電阻體積非常小,對溫度變化的響應也快。但半導體熱敏電阻需要使用電流源,小尺寸也使它對自熱誤差極為敏感。
半導體熱敏電阻采用的原理是溫度引起電阻變化。假設半導體熱敏電阻內部的電子和空穴的濃度大小為 n 和p,其電子和空穴在材料內部的遷移率分別為 u n 、μ p ,那么該半導體熱敏電阻的電導為:
σ=q(nμ n +pμ p ) (2)
由于 n、p、μ n 、μ p 都與溫度的大小有一定的關系,因此,當溫度變化的時候,半導體熱敏電阻的電阻大小也會發(fā)生一定的變化,并且這種變化有一定的規(guī)律,這就是半導體熱敏電阻的工作原理。
將半導體熱敏電阻接入電路以后,再將隨被測溫度變化的電壓或電流采集過來,進行 A/D 轉換后,接入處理器進行數(shù)據(jù)的處理,就可以得到環(huán)境溫度。這種設計需要用到 A/D 轉換電路,成本適中,但是非線性太大,使得后續(xù)的數(shù)據(jù)處理比較麻煩,互換性較差,非線性嚴重,測溫范圍只有-50℃-300℃左右,大量用于家電和汽車用溫度檢測和控制。
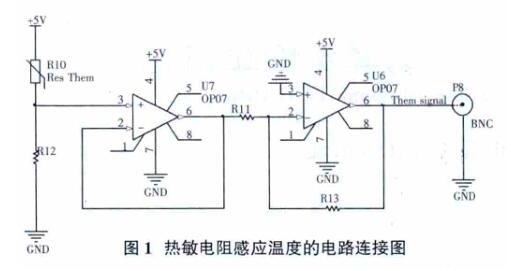
圖 1 是一種比較簡單的熱敏電阻的溫度電壓轉換電路。
1.2 采用經(jīng)典的鉑電阻
PT100 PT100 的電阻隨著溫度的變化會發(fā)生改變,不同的溫度對應不同的電阻值,電阻的重復性和穩(wěn)定性都較好,在程控制中的應用極其廣泛,其缺點是轉換電路較為復雜,往往需要采用電橋進行測量,成本較高。
一般對于金屬熱電阻而言,它的電阻值大小和環(huán)境溫度可以采用如下公式來進行換算,這個關系是采用了近似處理的,即:
R t =R t0 [1+α(t-t 0 )]
式中,R t 代表在環(huán)境溫度為 t 的情況下,金屬的電阻阻值;R t0 代表在環(huán)境溫度為 t 0 的情況下,金屬的電阻阻值,通常情況下,t 0 取 0℃,此時對應的電阻值為 R t0 ;α 為該金屬的溫度系數(shù)。
對于 PT100 來說,其連接方式有四線制和兩線制,四線制主要用于消除引線較長時產(chǎn)生的電阻誤差,而兩線制一般用在引線較短或溫度測量精度要求不高的場合;市場上有很多現(xiàn)成的 PT100 溫度變送器模塊,上面有接線端子,直接量 PT100 的引線接到溫度變送器上,溫度就能夠直接顯示,使用十分方便。
1.3 采用溫度數(shù)字式溫度傳感器 DS18B20
DS18B20是一種單總線溫度傳感器,其直接將溫度轉換為數(shù)字量,轉換的位數(shù)可在 9~12 位之間進行選擇,該溫度傳感器的誤差為 0.5℃,測量范圍在-55℃到 125℃之間,完全滿足工業(yè)現(xiàn)場料位測量的要求,線路連接簡單,價格也僅為 5 元每片,有較高的性價比。
2 超聲波傳播路徑修正
由于工業(yè)現(xiàn)場超聲波發(fā)射和接收模塊的安裝不可能在同一點,尤其是增加保護模塊以后,超聲波發(fā)射模塊和接收模塊是有一定距離的,因此超聲波的發(fā)射路徑和接受路徑不會是平行的,也并不相同,如果直接采用計算公式
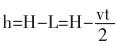
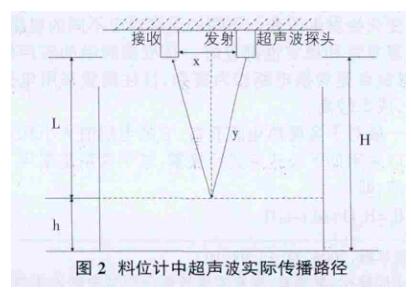
,當料位較低時,由于超聲波發(fā)射端和料位的表面距離較遠,因而傳播路徑也較遠,如果采用平行傳播路徑代替實際傳播路徑,此時產(chǎn)生的誤差相對較小;但在料位較高時,傳播路徑較短,誤差相對較大;因而采用實際的傳播路徑修正簡化的平行傳播路徑是十分必要的,這樣測量的液位才是準確的。其實際傳播路徑如圖 2 所示。
依據(jù)圖 2,假設超聲波發(fā)射信號從發(fā)射到接收的時間
2y=vt (4)
根據(jù)勾股定理可以得到
由圖 2 中的幾何關系可以進一步得到
h=H-L (6)
聯(lián)立式(4)、式(5)、式(6)可以得到非常終的液位關系表達式,這個計算公式是按照超聲波傳播的實際路徑進行推導的,準確度比公式
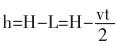
高
假設超聲波發(fā)射模塊和接收模塊安裝的距離為0.5m,和裝料容器底部的距離 H=10m,超聲波傳播速度為340m/s,傳播時間為 0.02s,超聲波那么依據(jù)公式和公式(7)計算的結果如下:
此時的誤差僅為 0.009m,這個值是相對較小的。但是如果傳播時間為 0.002s,再次依據(jù)公式
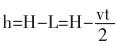
和公式(7)計算的結果如下:
此時的誤差就達到了 0.11m,相對于精度較高的料位測量來說,是不被允許的。