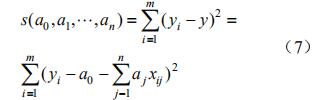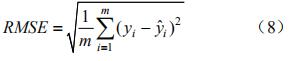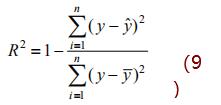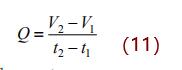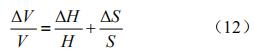摘 要:為了解決傳統水流量標準裝置存在由換向器的換入和換出行程差產生的流量測量誤差問題。通過對超聲波液位計的原理分析和容積標定法的研究,提出了一種基于超聲波液位計和標準水箱的流量在線檢測計量方法。利用超聲波液位計與標準水箱進行實驗,得到液位高度和液位體積的函數關系;利用上位機和 8 路模擬量采集模塊采集標準水箱液位高度和相應的時間,進而得到標準圓筒中液位體積和時間的關系,由單位時間內流體體積的變化值得到實際流量值。實驗結果表明,采用此方法得到的流量測量值精度能夠達到 0.55%,能夠實現流量的精準測量。
引言
流量計量與國民經濟和科學研究有著非常密切的聯系,它的準確測量對于提高生產效率、促進科學技術的發展具有非常重要的作用。通過計量確保流程工業在線不可拆卸計量儀表測量的準確性和可靠性是企業計量管理部門乃至國家計量院所面臨的重大課題。由于流量的動態特性使得流量測量技術變得更加困難和復雜。因此,為了更加準確地測量流體流量以及保證流量計量儀表的準確可靠性,必須選擇合適的流量測量方法。液位測量方法有很多,主要分為直接液位測量法和間接液位測量法。直接液位測量法是以直觀的方法檢測液位的變化情況,雖所用器具結構簡單但方法原始,不能滿足工業自動化的要求。因此間接液位測量法得到了廣泛的應用。在非接觸測量方式中超聲波流量計則具有計量精度高、對管徑的適應性強、靈敏度好、使用方便、易于數字化管理等優勢。
在現存的各種液位、流量儀表中,利用超聲技術研制的儀表因優越于其他
液位計、流量計,而且具有明顯優點(如可進行非接觸測量、測量精度較高等),在測量儀表中占有非常重要的地位,得到了越來越廣泛的應用[5]。正是由于超聲波流量計具有的諸多優勢,使得其成為了當今流量計量的主流[6]。事實上,基于超聲波液位計和計量槽測流量,在國內用的相當普遍,比如說農業灌溉水的流量測量,工廠排污口的流量測量,人工渠道的流量測量等。相比于多普勒測流法,這種方式測出來的精確度肯定沒有多普勒法的精確度高,但它也有它的存在價值。多普勒測流法對于水深、流速和水的清澈度是有要求的。而一旦水深比較淺,水比較清澈,流速很慢或者超快時,就需要超聲波液位計進行流量計量了。
由于測量原理的不同或測量元件的形式差別,每一種流量儀表都有其非常為適用的工況和獨特的安裝要求。在流量儀表的實際應用中,要想達到優良的測量效果,既要選擇合適的儀表類型,還要兼顧流量計安裝位置滿足所選儀表的測量要求。通常使用的流量計有節流式差壓流量計、渦街流量計、超聲流量計等,現有的超聲波流量計的精度為 1%,配置插入式傳感器準確度可達0.5%,為了確保流量測量方法的精度,本文提出了一種基于超聲波液位計和標準水箱的流量在線檢測計量方法。利用超聲波液位計測得標準水箱的液位高度 H 和液位體積 V 的數據,由非常小二乘法得到液位高度和液位體積的函數關系 V(H);利用 8 路模擬量采集模塊 DAQM-4206 進行數據傳輸,在基于 python 的上位機中得到每個時刻 t 對應的液位高度 H,進而得到每次實驗中體積 V 和液位上升時間 t 的函數關系 V(t),從而能實現流量的瞬時測量,則單位時間內流體體積的變化值就是實際流量值。
1 超聲波流量標定方法原理
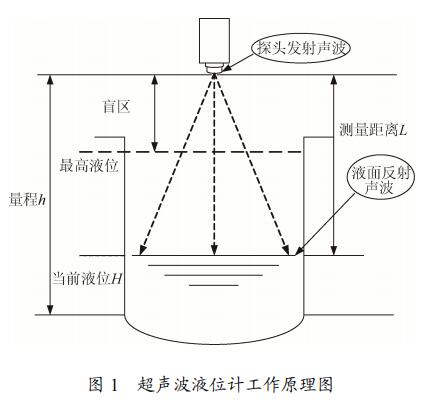
1.1 超聲波液位計工作原理
超聲波液位計是微處理器控制的數字液位儀表。由超聲波換能器、信號處理模塊、輸出單元 3部分組成。其工作原理圖如圖 1 所示。
在測量中超聲波換能器(探頭)發出高頻脈沖聲波,聲波經液體表面被反射折回后,反射折回的反射回波被換能器接收,通過壓電晶體或磁致伸縮器件轉換成電信號,并由聲波的發射和接收之間的時間來計算傳感器到被測液體表面的距離。實驗所用超聲波液位計的測距原理如下:
式中:h 為由超聲波傳感器到底部的距離;L 為傳感器到液面的距離;C 為超聲波聲速;H 為被測液面實際高度;T 為超聲波由發出到接收到的時間。實驗過程中,每次液位體積變化后,超聲波液位計測到的液位高度都可以直接顯示,直接讀數即可。
由于超聲波液位計采用的是非接觸測量,因此被測介質幾乎不會受到限制,可廣泛用于各種液體和固體物料高度的測量[8]。
1.2 非常小二乘法線性擬合原理
在參數估計以及曲線擬合問題中,要求確定某些或一個未知量,使它能夠對所測得的一組觀測值進行表征,通常在數據處理中采用非常小二乘法來解決這類擬合曲線問題。非常小二乘法是曲線擬合普遍采用的數學優化方法,可以匹配出數據變量的非常優函數組合,非常小二乘估計不要求觀測數據提供概率統計方面的信息,估計結果有很好的統計特性。
非常小二乘法通過計算非常小誤差的平方和來計算非常可信賴值。它不但可以用于線性參數的處理,也可以用于非線性參數的處理。非線性參數的處理需要用級數展開的方式把某一區域內近似的化成線性的形式。非常小二乘法能夠充分的利用誤差抵償作用,有效地減少隨機誤差帶來的影響。其殘差定義為:
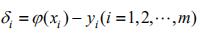
,其中φ(xi) 為擬合值,yi 為真實值,希望 δi 盡可能小,常見的方法有:
(1)選取ψ(x)使偏差的一范數非常小,即
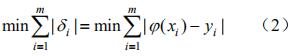
(2)選取ψ(x)使偏差的無窮范數非常小,即
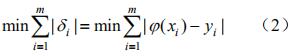
(3)選取ψ(x)使偏差的二范數非常小,即
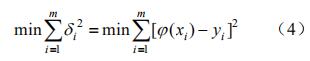
公式(4)被稱為非常小二乘法原則。
1.2.1 一元線性擬合
假設要對一組 N 個(xi,yi)樣本數據做 y=ax+b線性擬合,則擬合重點在于擬合出(a,b)的值。因此可以對每個樣本數據(xi,yi)做誤差求和計算,其定義為:err=Σ[yi–(axi+b)]2,并希望選取合適的 a 和 b 的值使 err 值非常小,因此,對誤差做偏微分計算。故有:
進而解出:
1.2.2 多元線性擬合
設變量 y 與 N 個變量 x 之間存在著一定的線性關系為:
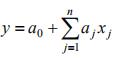
設變量 xj 的第 i 次測量值為 xij,對應的函數值為 yi(i=1,2,···,m),則偏差平方和
為使 s 取極小值,對式(7)求偏導,將實驗數據(xij,yj)代入可得出未知參數 α0, α1,···, αn。
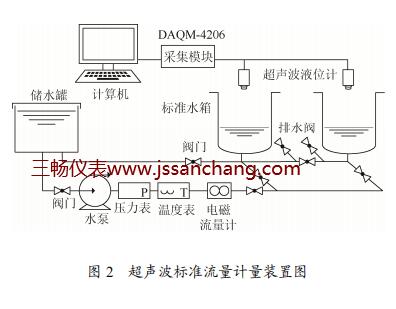
2 超聲波標準流量計量裝置
超聲波標準流量計量裝置是由標準水箱、超聲波液位計、信號采集裝置、計算機 4 部分組成。其超聲波標準流量計量裝置如圖 2 所示。
裝置中的水箱是兩個敞口式的圓柱形標準水箱,為了防止進水時,水面波動對超聲波液位計信號采集產生造成影響[13],把進水口放置在水箱底部并且把其底部設計成一個高度為 0.25 m 弧狀型緩沖區域,這樣就可以使水流通過緩沖區域流到測量區域時,水面近似于平穩,避免了水面波動造成的影響。采用的一體化 ZP-UF10M68 型超聲波液位計具有安裝方便,便于清潔維護的特點[14]。其測距分辨率為 1 mm;測距精度為 0.5%,適用于–20~+60 ℃的常溫環境中,測量盲區為 0.6 m。
為了滿足超聲波液位計的測量要求,使其測量精度更高,把超聲波液位計安裝在距離水箱頂部 0.6 m處。工業級 DAQM-4206 是一款標準模擬量采集產品,具有 12 位的分辨率,精度等級高達 2%,支持 0+5 V、1+5 V、0~20 ma、4~20 ma 量程 8 通道單端輸入。MODBUS 通訊更新速率達到 10 Hz,AD采樣率高達1 MHz,可以實現8通道同步采樣。把 8 路模擬量采集模塊 DAQM-4206 的模擬量輸入端與一體化 ZP-UF10M68 型超聲波液位計的4~20 ma 模擬量輸出端連接,另一端接 USB 轉 485串口線模塊實現與計算機的通信。采用基于python 的上位機進行數據采集和處理。
3 實驗結果及分析
3.1 實驗環境
本實驗裝置采用 80 mm 不銹鋼管道,一體化溫度變送器,智能電磁流量計,一體化 ZP-UF10M68型超聲波液位計,DAQM-4206 模擬量采集模塊等裝置,測得 14 組液位高度 H 和體積 V 的數據。采用 MALTAB 軟件編寫程序,利用非常小二乘法對采集到的標準水箱內液位高度 H 和體積 V 進行擬合。
3.2 建立液位體積 V 和液位高度 H 的關系
首先把兩個圓筒式水箱底部半圓弧狀的緩沖區域灌滿水,剛好到圓筒垂直底部,把此時水位設置為超聲波液位計的零點。把兩個水箱分別標記為 1 號水箱和 2 號水箱,保持 1 號水箱水位不變,把 2 號水箱注滿水。通過排水閥放出定量 2號水箱的水,記水的體積為 V,將這些水移到 1號水箱當中,分別記錄此時 1 號水箱和 2 號水箱的液位和對應體積的關系。按此方法分別測得 5 000 mL、7 000 mL、10 000 mL、12 000 mL、15 000 mL、17 000 mL 共 6 組液位體積變化數據。利用非常小二乘法擬合得到6個擬合曲線如圖3所示。
——————————
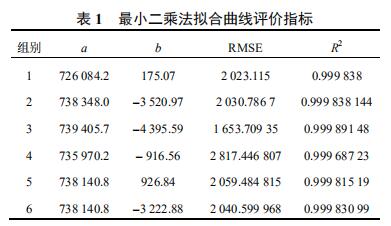
通過非常小二乘法得到線性擬合曲線方程式的形式為:y=ax+b,以均方根誤差 RMSE 和決定系數 R-squared 作為擬合曲線的評價指標。均方根誤差的計算公式如下:
可決定系數的計算公式如下:
可決定系數的范圍在 0~1 之間,其值越接近于 1 說明線性擬合程度越好,均方根誤差越小說明線性擬合程度越好,得到非常小二乘法擬合曲線評價指標數據如表 1 所示。
從表 1 中分析得出第三組數據的非常小二乘法擬合曲線得均方根誤差 RMSE 值 1 653.709 35 非常小,可決定系數 R-squared 值 0.999 891 48 非常接近于 1,因此非常后得到標準桶內液位高度 H 和體積 V的擬合曲線如下式所示。
V=739 405.7H-4395.59(10)
3.3 流量測量方法與誤差分析
對實驗數據進行非常小二乘法擬合得到液位高度H和體積V的擬合曲線V(H);由一體化ZP-UF10M68型超聲波液位計對液位高度進行采集,通過 8 路模擬量采集模塊 DAQM-4206 把數據傳輸到上位機,在基于 python 的上位機中可以得到每個時刻t 對應的液位高度 H,進而可以得到每次實驗中體積 V 和液位上升時間 t 的函數關系 V(t)。得到函數關系圖如圖 4 所示。
根據函數關系圖可以得知流量 Q 的計算公式如下:
式中:Q 為流量,mL/s。
根據 JJG 2263-2007 液體流量計量器具鑒定系統表規程,在測量過程中,工作量器允許的誤差不應超過 0.05%,在實驗過程中所使用的計量儀器的精度符合上述檢定規程,非常大測量體積為5 000 mL,非常大允許誤差為 15 mL,所使用的超聲波液位計量程為 0.45~10 m,精度為 0.5%,非常大允許誤差 A 為 0.047 75 m,由于測量結果主要受這兩方面誤差影響,它們之間的關系為:
式中:S 為水箱的橫截面積,因為水箱中液位的體積 V=SH,所以系統非常后合成的總誤差為 0.55%,由于超聲波液位計聲速的傳播速度與空氣壓力及環境的溫度有關,正常條件下由于大氣壓力變化很小因此其傳播速度主要考慮溫度的影響,在空氣中傳播速度為:
C=331.5+0.6t (13)
已知在實驗過程中溫度為 15 ℃,上下浮動非常大為 0.4 ℃,由此而產生的誤差為 0.07%,經上述補償公式得到的超聲波速度計算流速,對溫度造成的聲速變化進行補償,可有效提高測量精度,這種誤差是可以進行補償的。
由于超聲波液位計要經采集模塊與計算機進行通信,硬件電路延時等會產生系統誤差[15],因為系統誤差都是由于硬件電路本身引起的,而在實驗過程中,實驗環境以及硬件設施的配置都是相同的,因此,對于不同高度的液位進行測量時都存在時間延遲的情況,假設 S1、S2 為兩個待測的不同的液位高度,t1、t2 分別為對應于這兩個固定距離采集的回聲值(內含 Δt 因素),則超聲波在 S1、S2 距離內傳播所用的時間實際上分別為t1–Δt 和 t2–Δt。所以在計算時間的過程中 Δt 的影響可以抵消,也就是說時間的誤差的影響可以忽略不計。
4 結論
(1)針對水面波動對超聲波液位計測量的影響問題,設計了一個從底部進水并且具有半球狀緩沖區域的標準水箱,有效減小了水面的波動。
(2)提出了一種基于超聲波液位計和標準圓筒的流量在線檢測計量方法。建立了決定系數和均方根誤差為 0.999 891 48 和 1 653.709 35 mL 的液位體積和高度的擬合曲線,利用 8 路模擬量采集模塊 DAQM-4206 和基于 python 的上位機實現了流量的在線檢測。
(3)對實驗結果進行誤差處理,得到非常后的精度為 0.55%,進行溫度補償以后,精度可以達到 0.5%,符合現有超聲波液位計的測量精度,能夠實現流量的精確測量。




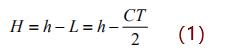
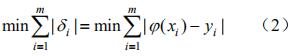
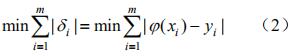
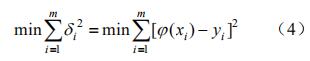
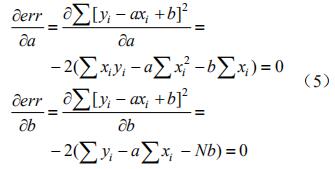
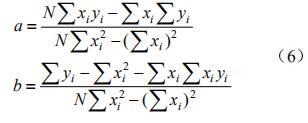
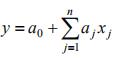 設變量 xj 的第 i 次測量值為 xij,對應的函數值為 yi(i=1,2,···,m),則偏差平方和
設變量 xj 的第 i 次測量值為 xij,對應的函數值為 yi(i=1,2,···,m),則偏差平方和